Un développeur logiciel chevronné mais qui venait de se mettre au développement sous iOS me demandait —avec quelques craintes — si un débutant avec quelques mois d’expérience pourrait être plus doué que lui.

Avant d’apprendre à conduire une voiture, on pense que la difficulté réside dans la manipulation des commandes: comme il semble compliqué de tourner le volant tout en appuyant sur les pédales et en actionnant le commodo du clignotant ! Voilà qui exige beaucoup de coordination pour ne pas entrer en collision avec les autres véhicules.

Après quelques semaines de conduite, on sait que la difficulté se trouve ailleurs: il s’agit essentiellement d’anticiper, de comprendre les intentions des autres usagers de la route et d’adapter ses gestes et sa vitesse pour éviter les obstacles et s’insérer dans le trafic.

Un conducteur aguerri qui changerait de type de véhicule — disons qui passerait de la voiture au scooter — serait bien évidemment déboussolé dans un premier temps, ne serait-ce que par l’équilibre, le placement des commandes, et les capacités d’accélération. Mais il s’y ferait rapidement, parce qu’il maîtrise les fondamentaux de la conduite.

Cela pour dire qu’un développeur expérimenté qui se mettrait au développement sous iOS serait désorienté au départ, peut-être par le langage Objective-C, le tactile, les multiples classes ou Xcode. Mais les fondamentaux sont déjà là: savoir gérer la complexité, trouver son chemin dans la documentation, avoir une méthodologie. Il peut s’attendre à être bon en deux ou trois mois.

Un débutant peut parvenir à créer une application et la publier sur l’App Store. Mais certainement pas une application seulement un peu complexe. Il lui manque trop de fondamentaux.

Lors de l’une de mes dernières formations pour Mediabox, j’ai posé une question qui me paraissait bien anodine: “Comment calcule-t-on la distance entre deux points” ? Je fus bien étonné qu’aucun de mes élèves ne sache répondre.

Les deux points sont placés dans un repère cartésien et leurs coordonnées sont connues. J’ai commencé par dessiner deux points aux tableau. En complétant le dessin, et en faisant de ces deux points des sommets d’un triangle rectangle, cela donne:

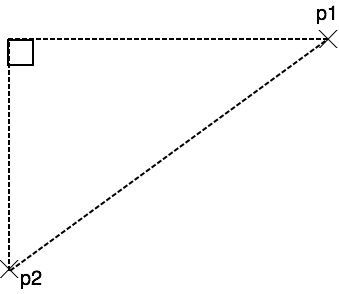
Une fois la figure tracée, une réponse me fut enfin donnée: “Il faut utiliser le théorème de Pythagore”. Exact.

Le calcul

La figure montre clairement que la distance est l’hypoténuse du triangle. D’après la réciproque du théorème de Pythagore:

distance = √(largeur^2 + hauteur^2)

Nous obtenons les largeurs et hauteurs par les coordonnées des points:

largeur = abs(p1.x – p2.x) hauteur = abs(p1.y – p2.y)

Il faut utiliser la fonction valeur absolue abs() parce que p2.x peut très bien être supérieur à p1.x. De même pour les y. Cependant, comme le carré d’un nombre réel est forcément positif, le code fera l’économie de l’appel à cette fonction abs().

Implémentation du calcul de distance

Passons donc au code en langage C:

#include <math.h>

typedef struct { 
 float x; 
 float y; 
} Point; 

float distancePoints(Point p1, Point p2) 
{
 float largeur = p1.x - p2.x;
 float hauteur = p1.y - p2.y; 
 return sqrtf(largeur*largeur + hauteur*hauteur); 
}

Quelques remarques sur l’implémentation:

on utilise la fonction sqrtf() et non sqrt() pour le calcul de racine carrée. Les fonctions mathématiques de math.h travaillent normalement sur des doubles et non des floats. Les fonctions adaptées aux floats, comme sqrtf() sont plus rapides.
on n’utilise surtout pas powf(largeur, 2), pour élever la largeur au carré. Une simple multiplication est très rapide comparée à un appel de fonction, encore plus comparée à cette fonction powf().

Réflexion sur notre métier

En fait, si j’en suis à vous donner ces explications, c’est parce qu’une fois la réponse donnée à mes élèves, l’un d’eux m’a dit: “À quoi bon savoir comment calculer une distance, je vais trouver la fonction toute faite sur le net en deux minutes”. Il me semble que l’argument que je lui ai donné à ce moment était mauvais, à savoir qu’il était important d’avoir une culture générale de l’informatique.

En y réfléchissant, j’ai commencé à programmer à une époque où Internet n’existait pas. Même les rares livres d’informatique ne donnaient pas forcément ce genre d’informations. À l’époque, je n’avais d’autres choix que me creuser la tête ou poser des questions à un prof de math ou de physique, voire parler avec d’autres programmeurs amateurs. L’avantage est que j’ai des connaissances variées, et que je peux revenir aux bases si besoin. Avec suffisamment de temps, peu de choses me paraissent infaisable. L’inconvénient est que j’ai tendance à réinventer la roue: plutôt qu’adopter une bibliothèque toute faite trouvée sur le net, je vais souvent préférer la programmer moi-même; elle sera ainsi plus flexible et plus adaptée à mes besoins, mais l’écrire va me prendre du temps.

Finalement, j’ai tout de même trouvé un bon argument. Voici un cas typique: on clique à la souris, et il faut sélectionner le point le plus proche. Pour ce faire, un algorithme simple consiste à calculer la distance entre tous les points du diagramme et les coordonnées du clic. Or, utiliser la fonction ci-dessus est lent. Une bien meilleure méthode est de comparer non pas les distances, mais les carrés des distances. On élimine ainsi l’appel à la fonction sqrt(), et on gagne énormément de temps! Mon argument est que si on utilise du code sans vraiment le comprendre, alors on n’en connait pas non plus les limites, et on ne peut pas l’adapter à ses besoins.